Realizing I needed to do a better job of balancing seriousness and casualness, here's a quick joke I came across the other day and just needed to share:
Person 1: How many avocados do I need to make guacamole?
Person 2: Avocado's number, 6.022E23 avocados/guacamole!
Seems like Trader Joe's is geekier than I thought:
OK, back to the draft for my next post, it's going to be a biggie!
Tuesday, January 29, 2013
Tuesday, January 22, 2013
From "Will they be champs?" to "Will they make the playoffs?"
I have not posted any basketball-related articles since sharing my data-driven predictions for the 2012 NBA Finals (unfortunately for me, the data suggested the Oklahoma City Thunder had a slight advantage against the Miami Heat).
But there has been SO much talk recently on the Los Angeles Lakers' performance that I just had to take a stab at predicting their season outcome.
Background
For those of you not too familiar with the situation, it has all the drama of a Hollywood script, and I will briefly summarize the situation.
The Lakers have had great results in the past years, winning the championship in 2009 and 2010, and being tough opponents in the other years. Over the 2012 summer and a disappointing 2012 year, they signed a couple of superstars: Steve Nash from Phoenix, desperate to win a championship and one of the league's top point guards, as well as Dwight Howard from Orlando, who can be quite a beast under the basket. On paper they were an All-Star team, nobody contested that. Almost everyone had them reaching the Finals, the only question was whether they would beat Miami or not.
But their performance so far surprised even the most pessimistic: they started the season by accumulating losses, and have lost more games than they have won since the start of the season. Things get worse as they are in the Western Conference which is much more competitive than the Eastern conference. Add in a fired coach, a surprising replacement coach, and you have all the drama necessary for a lot of ink to be poured!
Total confusion on the court has been a common sight in the Staples Center:
And so the questio has become: will the Lakers even make it to the NBA playoffs? Only the best eight teams of the Western conference make the playoffs. Many analysts have looked at historical data, noticing that the eight team in the West has an average of 48 wins, and if the Lakers want to reach 48 wins this season they need to start winning fast.
I've decided to take a slightly different approach, by tring to forecast what the rest of the season would look like for all teams based on the first half of the season. Also, the previous methodology ignores what the rest of the teams are doing in your conference, as well as the impact of playing another team also fighting for a playoff spot. When you win against one of those teams, it basically counts double!
Methodology
Here's the methodology I've taken:
- extract all of the 2012-2013 season scores and schedule data for all teams, namely home and away winning percentages
- for all upcoming games I compute the home team's probability of victory as follows:
home team winning percentage / (home team winning percentage + away team winning percentage).
For example: Let us say that Chicago with a 12-5 road record (70.8% road winning percentage) is visiting Miami with a 16-3 home record (84.2% home winning percentage), I would estimate Miami's probability of winning the game as:
84.2% / (84.2% + 70.8%) = 54.4%. - Based on this probability, I simulate the game's outcome and then update Chicago's and Miami's records (if Chicago wins, their road record is now 13-5 and Miami's home record becomes 16-4).
- I continue proceeding that way until all the season's games have been simulated. This then becomes one possible outcome for the season.
- I then repeat the entire process outlined above thousands of time to get an idea of all the scenarios that can play out.
Results
Here are the results (based on scores up to 21/01/2013):
Top three NBA records:
- First place:
Oklahoma City Thunder (32.9%), San Antonio Spurs (29.2%), Los Angeles Clippers (28%) - Second place:
San Antonio Spurs (26.6%), Oklahoma City Thunder (24%), Los Angeles Clippers (23.4%) - Third place:
San Antonio Spurs (18.7%), Oklahoma City Thunder (17.6%), Los Angeles Clippers (17.1%)
As for the Lakers, here are the probabilities of their final standing in the Western conference:
| Position | Probability |
|---|---|
| 6 | 0.4 |
| 7 | 1.4 |
| 8 | 4.1 |
| 9 | 8.9 |
| 10 | 12.6 |
| 11 | 18.1 |
| 12 | 24.2 |
| 13 | 16.9 |
| 14 | 10 |
| 15 | 3.4 |
Wow! Only a 5.9% probability of the Lakers making the Playoffs!
But let's still monitor them closely, and I'll update these results in the weeks to come.
Please leave a comment if you have any questions/suggestions on the methodology and/or results!
Labels:
2012,
2013,
champions,
forecasting,
kobe bryant,
lakers,
lebron james,
los angeles lakers,
miami,
NBA,
nba playoffs,
nba standings,
oklahoma,
playoffs,
quantitative,
regression,
standings,
statistics,
thunder
Monday, January 21, 2013
2013: Year of Statistics (and this blog!)
Quick post to remind everyone that 2013 is officially the year of statistics!
The official site is http://www.statistics2013.org/, and has tons of information on what statistics are (not just for sports) and what statisticians do (not just bore people at parties).
If you only want a two-and-a-half minute overview of how cool statistics are, than here's the summary video:
http://www.youtube.com/watch?feature=player_embedded&v=nTBZuQR7dRc
It's been a quick post I agree, but I'm working on quite a bunch of stuff I'm hoping to add really soon!
Tuesday, January 15, 2013
Does chocolate consumption increase the number of articles on correlation VS causation?
On October 18th 2012, the New England Journal of Medicine published a paper linking chocolate consumption and Nobel prizes by country. I’m sure you’ve heard about the study, it went pretty much viral after that, people found it cool to post and re-post on Facebook, Twitter…
There have also be countless articles on the topic, and while the methodology and approach of the original paper are highly debatable (and actually there is quite some talk about the paper being a joke from the New England Journal of Medicine), I still found something very troubling in how the results of the paper were paraphrased amongst journalists and friends.
To recall the setup, Franz Messerli (happens to be Swiss), looked at chocolate consumption per capita and number of Nobel Laureates per 10 million people across 23 countries, and found the following results:
All 23 data points, with the slight exception perhaps of Sweden and Germany, seem to fall on a straight line! And Pearson’s correlation coefficient of 0.791 is statistically significant!
I haven’t read the paper myself but the last part seems to attempt to explain the phenomenon, namely by the increased cognitive abilities derived from higher chocolate intake.
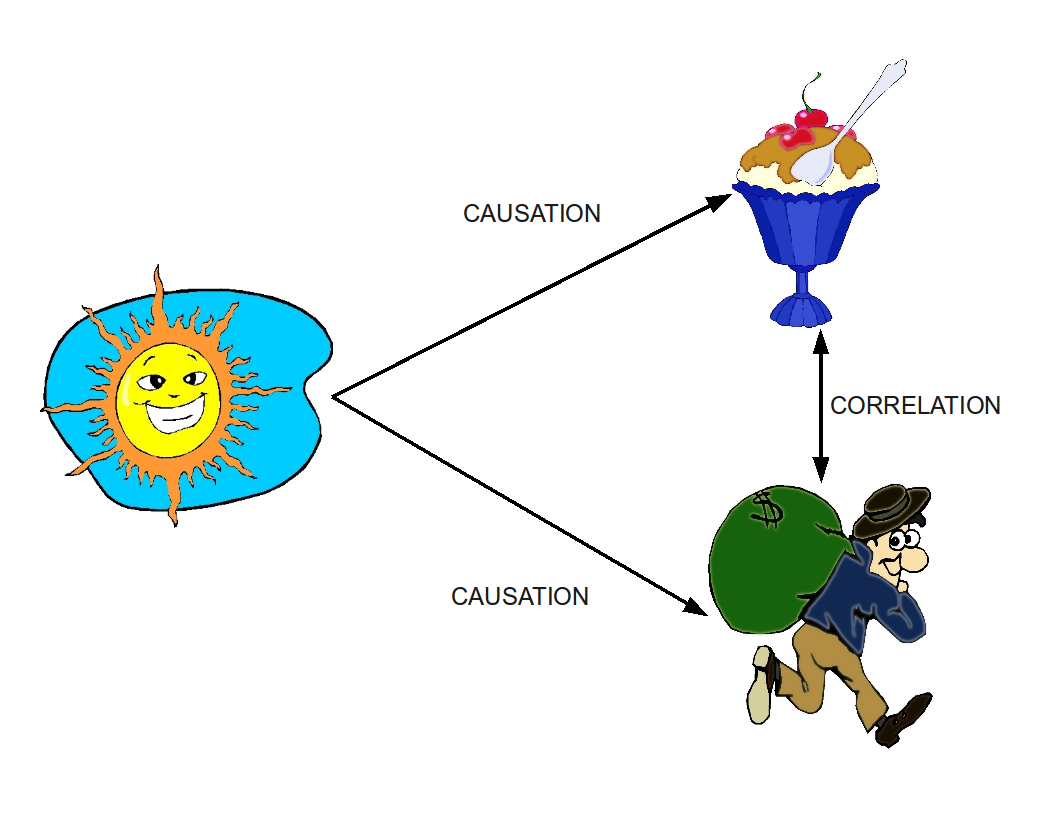
Of course, journalists need to shoot for the sensational, but the misunderstanding between correlation and causation is a very real and widespread one, and so I thought I would use the Chocolate / Nobel Prize example to illustrate how the two concepts differ.
- The first hypothesis could be that this was just a random coincidence and that countries not satisfying the “model” were dropped out (think of all the top IQ countries).
- An alternative (third variable) could be that countries in northern Europe tend to eat more chocolate and tend to have more laureates per capita. Do they have longer and colder winters? Because of the long winters you tend to eat more chocolate to improve morale? Because of the long winters you tend to eat spend more time studying than if you had a warm sunny beach outside? And haven’t sociologists linked long cold winters to increased suicide rates and crimes? (this is what led me to take a closer look at crime-related variables)
To do so, I will first replicate the original analysis as closely as possible, but also look at some additional metrics.
I was not able to pull the original dataset, so searched the web as best as I could to find chocolate consumption numbers and Nobel prizes per capita.
As boasted in the paper, I also got a great correlation, albeit not as significant (0.658 instead of 0.791). First little red flag, it appears that the number is quite volatile and rather data-sensitive. While it is hard to lie about Nobel Prize laureates, one might wonder if there even is anything such as an official chocolate consumption database?
Step 2 consisted in looking at another metric which is theoretically tied to Nobel Prize winning according to the paper: cognitive ability. Of course the first proxy that comes to mind for this metric is IQ. I therefore replicated the analysis looking at correlation between chocolate consumption and IQ.
Wow, the value dropped to 0.279! Even more troubling: only one of the top top IQ countries (Japan) was from the original analysis as there was no chocolate consumption data for them. Second red flag: why were only 23 countries included in the original paper?
So chocolate makes you smart enough to win a Nobel, but not enough to increase IQ?
But why settle on Nobel prize laureates and IQ, why not look at a whole set of metrics and test their correlations with chocolate consumption? With feminine intuition from my wife, I started focusing on crime-related metrics, and here are the results:
Kidnappings, correlation = 0.11
Drug offenses, correlation = 0.42
Rape victims, correlation = 0.45
What about total crimes per capita?
Correlation of… 0.72 !!! Even higher than for Nobel Prize! Stop eating that chocolate right now, or you will end up in jail before you know it!
So taking a step back, what have we shown? Well the first point is that if you compare enough metrics to each other, you are bound, just out of pure chance to come up with high correlation that does not mean anything. Just like if you flip a coin enough time (in the sense of quit your job right now) you are bound to get 20, 30 even 100 consecutive heads. Does it mean anything? No, you just lost your whole life for nothing.
The second important point is that there could be some link between the two metrics in question. But it does not mean that metric 1 impacts impact 2! Nor does it mean than metric 2 impacts metric 1! (the article never wonders whether Nobel prize laureates could have enough appetite for chocolate to lower their countries average consumption value). It could very well be that there is a third metric impacting both metric 1 and metric 2. The example I like best from my stats class is: does carrying a lighter increase your risk of getting lung cancer? Of course not why would it? Even if I told you there was a strong correlation between the two? Hmmmm. But here’s the thing, you are actually without knowing it comparing smokers to non-smokers. Smokers tend to have a greater probability of carrying lighters around, and of having greater risk for lung cancer. But carrying a lighter does cause lung cancer, and having lung cancer certainly doesn’t make you more prone to carrying a lighter!
OK, back to chocolate. What’s going on behind the scenes and behind the nice straight line? As discussed previously, there could be one of two phenomena going on:
Go ahead and eat all the chocolate you want, but hold off on booking that flight to Oslo…
I would also like to point out this article by James Winters and Sean Roberts which features a surprisingly similar analysis to mine (looking at IQ then at serial killers). Nobody copied anybody, I was just relieved to see I wasn’t the only one finding for correlation VS causation!
Subscribe to:
Posts (Atom)